判断点在有向线段的左（右）侧

要判断平面内一个点位于有向线段的左侧还是右侧，可以结合向量叉乘、向量点乘的代数和几何意义来进行计算判断。

数学基础

$$\vec{a}=(x_1,y_1,0)\\ \vec{b}=(x_2,y_2,0)$$

向量点乘

两个向量点乘的结果是一个标量，有以下两种算法。

• 代数

$$\vec{a}\cdot\vec{b}=x_1 \cdot x_2+y_1 \cdot y_2$$

• 几何

$$\vec{a}\cdot\vec{b}=\lvert{a}\rvert \cdot \lvert{b}\rvert \cdot cos\theta\\ \theta:向量\vec{a}和\vec{b}之间的夹角，\theta\in[0,\pi]$$

向量点乘的正负号有重要意义：

$$\vec{a}\cdot\vec{b}=0：cos\theta=0，\theta=\frac{\pi}{2}\\ \vec{a}\cdot\vec{b}>0：cos\theta>0，\theta\in[0,\frac{\pi}{2})\\ \vec{a}\cdot\vec{b}<0：cos\theta<0，\theta\in(\frac{\pi}{2},\pi]$$

实际使用时，通常通过代数计算两向量的点乘结果，根据该结果的正负来做几何上的判断。

向量叉乘

两个向量叉乘的结果是一个向量，有以下两种算法。

• 代数

$$\vec{a}\times\vec{b}=(0,0,x_1y_2-y_1x_2)$$

• 几何

$$\vec{a}\times\vec{b}=(\lvert\vec{a}\rvert\lvert\vec{b}\rvert sin\theta)\vec{n}\\$$

模：$\lvert\vec{a}\times\vec{b}\rvert=\lvert\vec{a}\rvert \cdot \lvert\vec{b}\rvert \cdot sin\theta\\$

方向：为$\vec{n}$的方向，遵守右手螺旋法则，右手握拳，四指沿$\vec{a}$、$\vec{b}$环绕，则大拇指所指方向就是结果向量的方向。

点在左（右）侧时的向量叉乘区别

• P在AB左侧时：

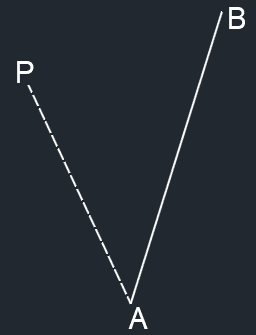
$$\vec{AB}\times\vec{AP}的方向垂直于纸面向外$$

• P在AB右侧时：

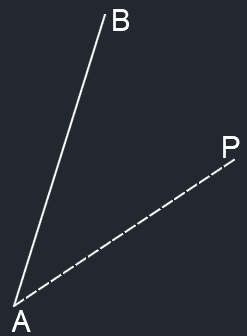
$$\vec{AB}\times\vec{AP}的方向垂直于纸面向里$$

• 结论：P在AB左侧时，AB和AP向量叉乘的结果向量垂直纸面向外；P在右侧时，垂直纸面向内。

结合向量点乘进一步推导

前面已知，当两个向量的点乘结果大于零表明两个向量之间的角度不大于90°。

那么要判断一个向量是垂直纸面向外（向内），我们可以将该相连与（0,0,1）向量进行点乘，结果大于零表明垂直纸面向外，小于零表明垂直纸面向内。

$$\vec{z}=(0,0,1)\\ (\vec{a}\times\vec{b})\cdot\vec{z}=(0,0,x_1y_2-y_1x_2)\cdot(0,0,1)=x_1y_2-y_1x_2$$

所以，判断平面内一个点位于有向线段的左侧还是右侧，其整体逻辑如下：

$$x_1y_2-y_1x_2>0:AB与AP叉乘结果，垂直纸面向外，P在AB左侧\\ x_1y_2-y_1x_2<0:AB与AP叉乘结果，垂直纸面向内，P在AB右侧$$